Rubik’s Cube ကို ကျွန်တော်တို့အားလုံး ရင်းနှီးကြပါတယ်။ ငယ်ငယ်တုန်း ကတော့ “မသိဘူး လှည့်မယ်” ဆိုပြီး လျှောက်ဆော့ ခဲ့ကြတာပေါ့။ နောက်ပိုင်း internet တွေ ဘာတွေ သုံးတတ်လာတော့ “How to solve Rubik’s cube” ဆိုပြီး ရိုက် ရှာရတာပေါ့လေ။ ပြီးတော့ သူငယ်ချင်း အချင်းချင်း ပြန်သင်ပေးကြနဲ့ ဟုတ်နေတာပဲ။

ဆိုတော့ …. Rubik’s cube ရဲ့ puzzle က သင်္ချာ ပုစ္ဆာ တစ်ပုဒ် ပါ လို့ ပြောရင် သင်ငြင်းမှာ မဟုတ်ပါဘူး။ ဒီ article မှာ 3 x 3 x 3 Rubik’s cube ရဲ့ သင်္ချာကို ဖော်ပြသွားပါမယ်။ ဘယ်လို solve လုပ်ရလဲ ဆိုတာကို ပြောမှာတော့ မဟုတ်ပါဘူး။
သူ့မှာ ဖြစ်နိုင်တဲ့ possible arrangement ဘယ်နှခု ရှိလဲ ဆိုတာကို တွက်ပြမှာပါ။ အရမ်း level မြင့်တဲ့ university level Mathematics တွေ မပါ ပါဘူး။ High school level Math နဲ့ တွက်လို့ရပါတယ်။
ဘာမှ စမပြောခင် factorial ဆိုတာ နဲ့ မိတ်ဆက်ပေးဖို့ လိုပါတယ်။ 4! ကို 4 factorial လို့ ဖတ်ပါတယ်။ “!” ဟာ factorial ပါ။ အာမေဍိတ် မဟုတ်ပါဘူး။
A, B, C, D ဆိုပြီး alphabet 4 လုံး ရှိတယ်ဆိုပါစို့။ သူ့ကို ABCD လို့ စီလည်းရတယ်။ BCAD, DBAC, CBAD, CDAB ဆိုပြီး ကြိုက်သလို စီ လည်းရတယ်။ ဒါဆိုရင် possible arrangement စုစုပေါင်း ဘယ်နှခုရှိလဲ? 4! ရှိပါတယ်။
4! = 4 x 3 x 2 x 1 = 24
Factorial ကို မိတ်ဆက် ပြီးပြီ ဆိုတော့ Rubik’s cube ကို သွားလို့ရပါပြီ။
Rubik’s cube ကို ကစားဖူးတဲ့ သူတိုင်း သိမှာပါ။ Center မှာ ရှိတဲ့ အရောင်တွေက fixed ဖြစ်နေပါတယ်။ သင့် အနေနဲ့ cube ကို ဘယ်လို လှည့်လှည့် center က ကောင်တွေက fixed ပါ ၊ နေရာ မရွေ့ ပါဘူး။ ဒါဆိုရင် ကျွန်တော်တို့ တွက်ချက်မှုမှာ center တွေကို ထည့် စဉ်းစား စရာ မလိုပါဘူး။
ဒါဆိုရင်… Rubik’s Cube ကို တစ်စစီ ဆွဲဖြုတ်လိုက်ပြီ လို့ စိတ်ကူးယဉ် လိုက်ပါ။ ပြီးရင် corner (ထောင့်) တွေကို အရင်စဉ်းစား ကြည့်တာပေါ့။ Corner မှာ ထည့်နိုင်တဲ့ piece က 8 မျိုးရှိပါတယ်။ 8 possible choice ပေါ့။ Corner (ထောင့်) နေရာက 8 နေရာ ၊ ရှိတဲ့ piece က 8 တုံး ဆိုတော့ possible arrangement က ဘယ်နှခု ဖြစ်မလဲ? အဖြေက 8! ပါ။
8! = 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1
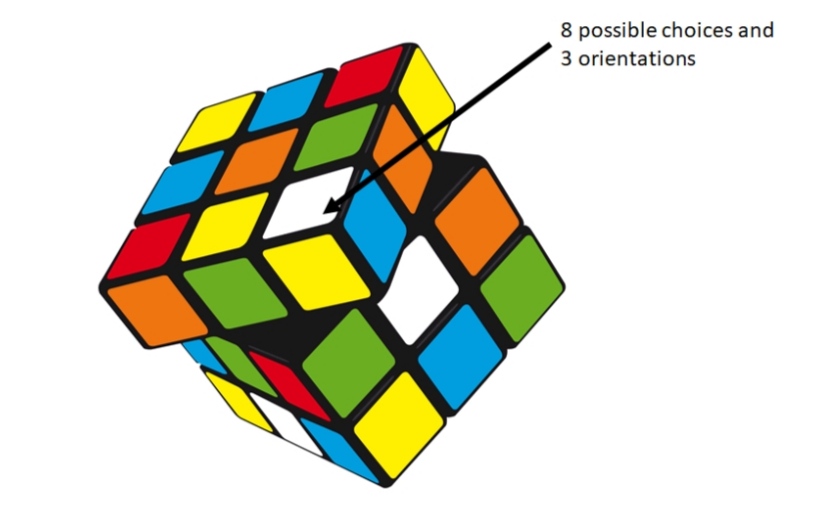
ဒါပေမယ့် corner က ကောင် တစ်ခုချင်းစီမှာ မျက်နှာပြင် 3 ဖက် ရှိနေပြန်ရော။ ဆိုလိုတာက သူသည် orientation သုံးမျိုး ဖြစ်နိုင်တယ်ပေါ့။ Orientation က 3 မျိုး စီကို 8 ခါ ဖြစ်နိုင်တယ်ဆိုတော့ 3⁸ ပေါ့။ (Corner cube က 8 တုံးရှိလို့ 8 ခါ ဖြစ်နိုင်တယ်လို့ ပြောတာပါ) ဒါဆိုရင် corner pieces တွေ အတွက် ဖြစ်နိုင်တဲ့ all possible arrangement တွေက –
All possible combinations for corner pieces = 8! x 3⁸
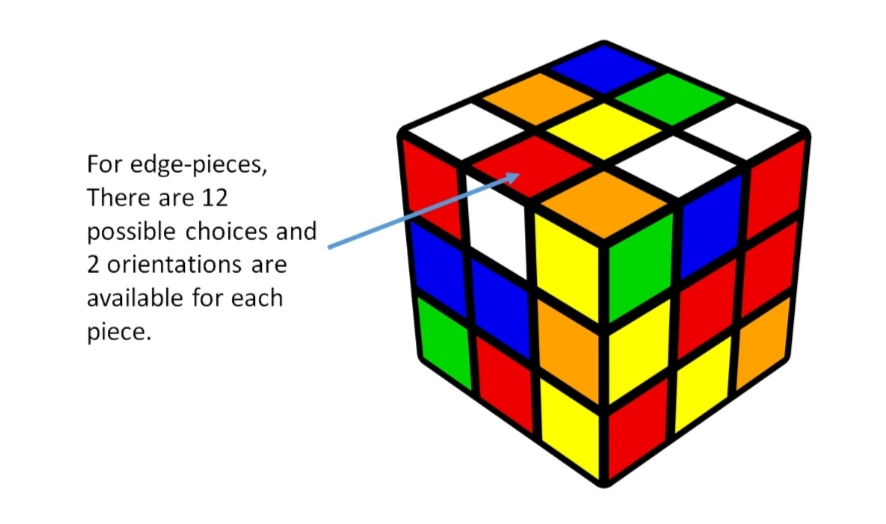
Corner ပြီးရင် အနားစောင်းက edge pieces တွေကို ဆက်စဉ်းစား ကြည့်တာပေါ့။ အနားစောင်းမှာတော့ piece က 12 မျိုး ရှိပါတယ်။ ဒါဆိုရင် ထုံးစံ အတိုင်း possible arrangement ကို စဉ်းစားရင် 12! ပေါ့။
ဒါပေမယ့် မျက်နှာပြင်ရဲ့ orientation ကိုလည်း ထည့်စဉ်းစား ရဦးမယ်။ မျက်နှာ ပြင်က 2 ဖက်ဆိုတော့ ဖြစ်နိုင်တဲ့ orientation က 2 မျိုးပေါ့။ Orientation က 2 မျိုး ၊ 2 မျိုး စီ 12 ခါ ဖြစ်နိုင်တော့ 2¹² ပေါ့ဗျာ။ ဒါဆိုရင် edge pieces တွေ အတွက် ဖြစ်နိုင်တဲ့ all possible arrangement တွေက –
All possible combinations for edge pieces = 12! x 2¹²
Corner piece တွေလည်း စဉ်းစား ပြီးပြီ ၊ edge က piece တွေလည်း ပြီးပြီ ၊ center က piece တွေက ထည့် တွက် စရာမလိုဘူး ဆိုတော့ ကျွန်တော်တို့ အဖြေ ရပါပြီ။
All possible combinations for a 3 x 3 x 3 Rubik’s cube = 8! x 3⁸ x 12! x 2¹²
But, wait! ဒါက နောက်ဆုံး အဖြေ ဟုတ် မနေသေးဘူး။ ဘာကြောင့်လဲ ဆိုတော့ မဖြစ်နိုင်တဲ့ condition တွေ ပါနေတယ်။ အောက်မှာပြထားတဲ့ ပုံတွေဆို မဖြစ်နိုင်တဲ့ အနေအထားတွေပေါ့။ ကစားဖူးတဲ့ သူတွေ သိပါတယ်။
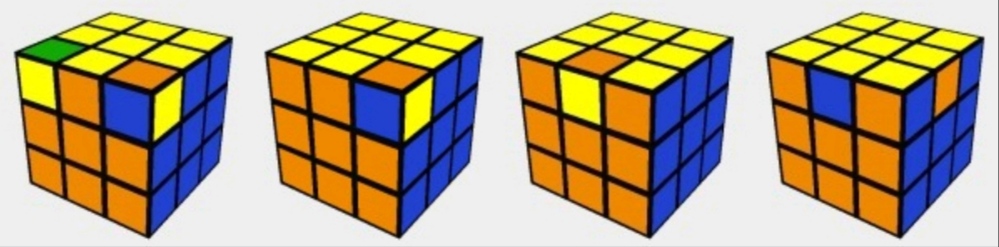
Corner cube တစ်ခု တည်း ကွက်ပြီး လွဲနေတာမျိုး မဖြစ်နိုင်ဘူး။ ဒါကြောင့် ဖြစ်နိုင်တဲ့ possible arrangement က 3 ပုံ တစ်ပုံ ပဲ ကျန်မယ်။ (3 နဲ့ စားရမှာပေါ့) နောက်ဆုံး corner cube ရဲ့ orientation က ရှေ့က 7 တုံးပေါ်မှာ dependent ဖြစ်လို့ပါ။ Edge piece လည်း ဒီလိုပါပဲ။ နောက်ဆုံး edge cube ရဲ့ orientation က ရှေ့က 11 တုံးပေါ်မှာ dependent ဖြစ်ပါတယ်။ ဒါကြောင့် possible arrangement ကို 2 နဲ့ ထပ်စားပါမယ်။ ပြီးတော့ edge piece 2 ခု က swap ဖြစ်နေလို့လည်း မရဘူးဗျ။ ဒါကြောင့် 2 နဲ့ ထပ်ပြီး စားရဦးမှာပဲ။ ခုမှသာ ကျွန်တော်တို့ရဲ့ နောက်ဆုံး အဖြေကို ရတာပါ။
All possible combinations for a 3 x 3 x 3 Rubik’s cube = (8! x 3⁸ x 12! x 2¹²) / (3 x 2 x 2)
ဒါ ကြီးကို calculator ထဲ ထည့်တွက်ရင် 43,252,003,274,489,856,000 လို့ အဖြေရပါလိမ့်မယ်။ (နည်းနည်းနောနော တော့ မဟုတ်ဘူး) 4.325 x 10¹⁹ လောက်ကိုရှိတာ။ အသေးစိတ် ထပ်ပြီးလေ့လာချင်သေးတယ်ဆိုရင် ဒီ link မှာ ကြည့်နိုင် ပါတယ်။ https://youtu.be/QV9k6dRQQe4
အဆုံးထိ ဖတ်ပေးတဲ့ အတွက် ကျေးဇူးတင်ပါတယ်။
-Uranium-
အသိအမြင်၊ အတွေးအခေါ် အသစ်တစ်ခုခုရသွားလို့ လှူဒါန်းလိုပါက Science Nuts (Facebook Page) ကို ဆက်သွယ်လှူဒါန်းနိုင်ပါတယ်။
လှူသမျှငွေအကုန်လုံးကို လိုအပ်တဲ့နေရာတွေမှာ ပြန်လည်လှူဒါန်းပေးသွားမှာပါ။